问题 B: [NOIp2008 提高组] 火柴棒等式
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:23
解决:0
题目描述
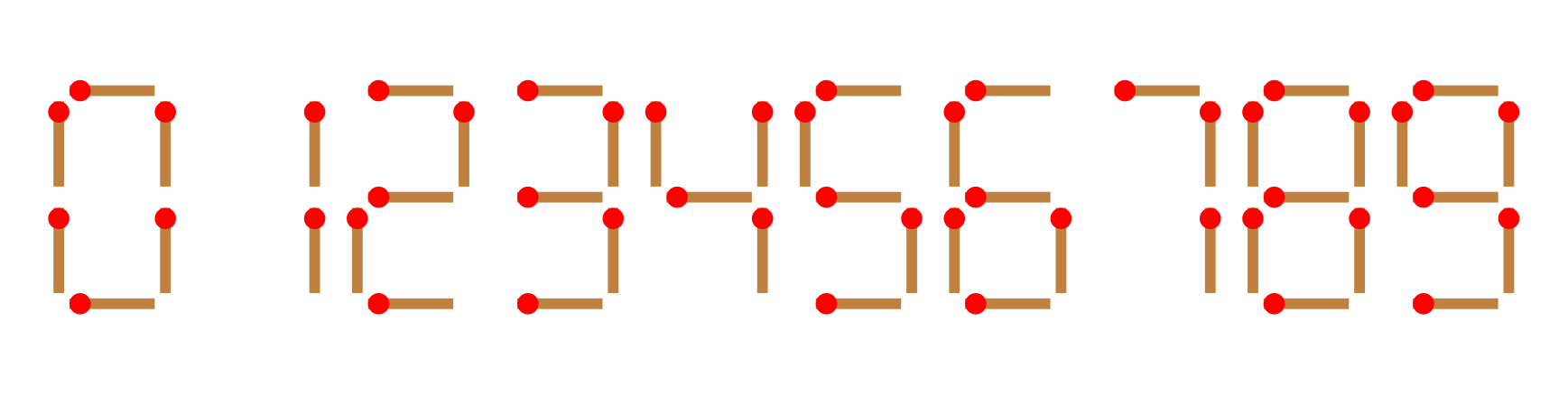
给你 $n$ 根火柴棍,你可以拼出多少个形如 $A+B=C$ 的等式?等式中的 $A$、$B$、$C$ 是用火柴棍拼出的整数(若该数非零,则最高位不能是 $0$)。用火柴棍拼数字 $0\sim9$ 的拼法如图所示:
注意:
1. 加号与等号各自需要两根火柴棍;
2. 如果 $A\neq B$,则 $A+B=C$ 与 $B+A=C$ 视为不同的等式($A,B,C\geq0$);
3. $n$ 根火柴棍必须全部用上。

输入
一个整数 $n(1 \leq n\leq 24)$。
输出
一个整数,能拼成的不同等式的数目。
样例输入 复制
14样例输出 复制
2提示
【输入输出样例 1 解释】
$2$ 个等式为 $0+1=1$ 和 $1+0=1$。