问题 I: 有依赖的背包问题
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:18
解决:0
题目描述
有 $N$ 个物品和一个容量是 $V$ 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
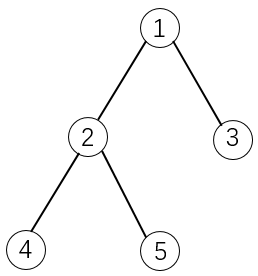
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 i,体积是 $v_i$,价值是 $w_i$,依赖的父节点编号是 $p_i$。物品的下标范围是 1…N。 求
解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入
第一行有两个整数 N,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 N 行数据,每行数据表示一个物品。
第 i 行有三个整数 $v_i$,$w_i$,$p_i$,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 $p_i$=−1,表示根节点。
数据保证所有物品构成一棵树。
输出
输出一个整数,表示最大价值。
样例输入 复制
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2样例输出 复制
11提示
数据范围
1≤$N$,$V$≤100
1≤$v_i$,$w_i$≤100
父节点编号范围:
内部结点:$1$≤$p_i$≤$N$;
根节点 $p_i$=$−1$;