1265: [STT2024WCR2] 柳树
内存限制:512 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:5
解决:2
题目描述
柳树(Willow)是一种树形结构,它的叶节点距离主干有一个距离,这个距离称为**绦长**。所有的绦长不少于一个定值,我们将这个定值称为**整棵树的绦长**。在叶节点的绦长范围之内,不会有其它分杈的枝桠。同时,柳树至少有三个叶结点。下图所示的是一棵绦长为 $2$ 的柳树。
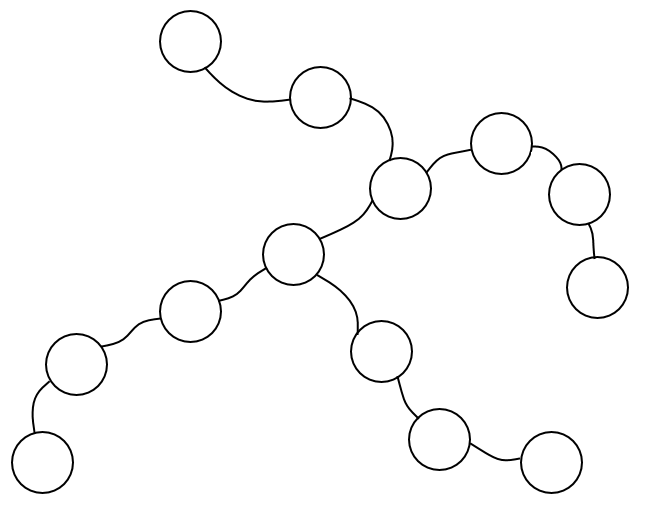
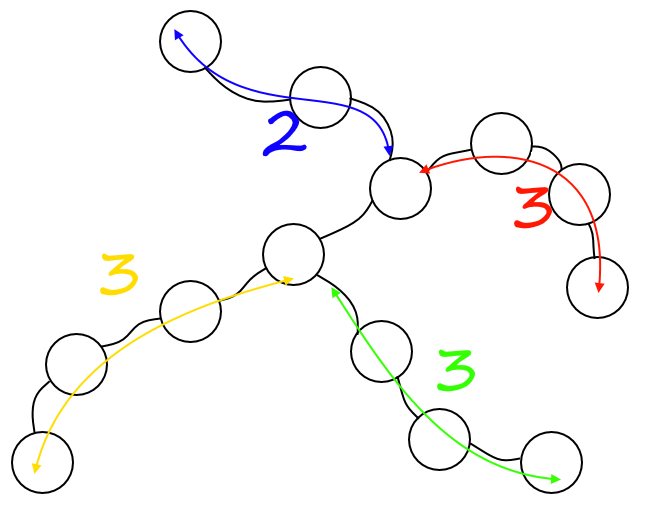
整棵柳树的绦长是由最短的那一条决定的。
给定一棵树,判断它是不是柳树。如果是柳树,还需求出这棵柳树的绦长。
输入
第一行一个整数 $T$,表示数据组数。
每组数据第一行一个正整数 $n$,表示树的结点个数。
接下来 $n-1$ 行,每行两个数 $u_i, v_i$ 表示 $u_i$ 和 $v_i$ 之间有连边。
输出
对于每组数据输出一行,如果这棵树不是柳树,输出`No`,否则输出整棵柳树的绦长。
样例输入 复制
1
13
1 2
1 3
1 4
2 5
2 6
3 7
4 8
5 9
6 10
8 11
7 12
10 13样例输出 复制
2提示
### 样例 #2
#### 样例输入 #2
```
2
4
1 2
2 3
3 4
12
1 2
2 3
2 4
4 5
8 1
5 9
3 10
9 7
8 6
11 10
6 12
```
#### 样例输出 #2
```
No
3
```
### 提示
**【样例 #1 解释】**
这个就是【题目描述】中的例子。
**【样例 #2 解释】**
第一棵树只有两个叶结点,所以不是柳树。
第二棵树是柳树,它有三条绦,绦长分别是 $3,3,4$,所以整颗柳树的绦长是 $3$。
**【数据范围】**
记 $\sum n$ 为数据中所有 $n$ 的和。
|子任务|分值|$\sum n \leq$|特殊性质|
|:-:|:-:|:-:|:-:|
|$1$|5|$50$|无|
|$2$|10|$10^3$|无|
|$3$|20|$10^6$|$A$|
|$4$|20|$10^5$|$B$|
|$5$|45|$10^6$|无|
特殊性质 $A$:是一颗二叉树;
特殊性质 $B$:叶子节点少于 $20$ 个。